La integral indefinida, conjunto de las infinitas primitivas que podría contener una función.
PROPIEDADES DE LA INTEGRAL INDEFINIDA
1) La integral del producto de una constante por una función es igual a la constante por la integral de una función.
∫ Kf(x) dx = k ∫ f(x) dx
2) La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫ [ f(x) + g(x) ]dx = ∫ f(x) + ∫ g(x)dx
La integral indefinida se representa de las siguientes formas:- Se representa por ∫ f(x) dx.
- y se lee integral de f de x diferencial de x.
- ∫ significa que es el signo que representa la integración.
- f(x) es la función integrar.
- dx el diferencial dx encargado de indicar cual es la variable que se integra en una función.
- C es la constante de la integración pero así mismo puede tomar cualquier valor numérico.
- Si F(x) es primitiva de f(x) dará entonces: ∫ f(x)dx = F(x) + C.
- Para verificar la primitiva y saber si es correcta suficiente seria con derivarla.
VIDEO DE AYUDA
INTEGRACIÓN POR PARTES
Cuando el integrado esta formado por un producto , se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
a pesar de ser una forma o método sencillo se debe aplicar de forma correcta.
1) El integrando debe ser un producto de dos factores.
2) Uno de los factores será u y el otro será dv.
3) Se calcula du derivando u y se calcula v integrando dv.
4) Se aplica la formula
- Para que esto funcione se debe escoger correctamente la u y dv, ya que una mala elección puede complicar la integración.
- No cambiar de elección, ya que hay veces que debemos aplicar el mismo método mas de una vez para calcular la misma integral.
- Integrales cíclicas, varias veces se ha dado que al aplicar dos veces la integración por partes luego debemos despejar la propia integral de la igualdad ya obtenida para poder calcularla.
EJERCICIO DE INTEGRACIÓN POR PARTES
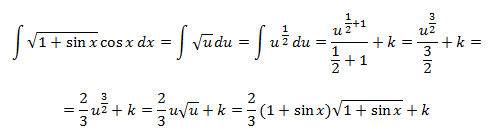


No hay comentarios.:
Publicar un comentario